Digital Signature Schemes

Direct Digital Signature

  • A digital signature scheme that involves only the communicating parties

    • Assuming the destination knows the public key of the source

  • Confidentiality is provided by encrypting the entire message & signature w\/ a shared secret key

    • Perform signature function first then an outer confidentiality function

    • In case of dispute: a third party must view the message and its signature

  • Validity of the scheme depends on the security of the sender’s private key

    • If a sender later wishes to deny sending a particular message, the sender can claim that the private key was lost or stolen and that someone else forged his or her signature

    • One way to thwart or weaken this ploy is to require every signed message to include a timestamp and to require prompt reporting of compromised keys to a central authority

Elgamal

  • PK for encryption (signing), PU for decryption (verification)

  • Global elements: q (prime number), a (primitive root of q)

  • Each user generates their key

    • Chooses a secret key (number): 1 < xA < q-1

    • Compute their public key: yA = $$a^{xA}$$ mod q

Schnorr

  • Based on discrete algorithms

  • Minimizes message-dependent computation required to generate a signature

    • Multiplying a 2n-bit integer with an n-bit integer

  • Main work can be done during idle time of the processor

  • Based on using a prime modulus p, with p-1 javomg a prime factor q of appropriate size
    • Typically p is a 1024-bit number, a is a 160-bit number

NIST Digital Signature Algorithm (DSA)

  • Based on difficulty of computing discrete logarithms and schemes originally presented by Elgamal [ELGA85] and Schnorr

  • Published by NIST as Federal Information Processing Standard (FIPS) 186

  • Uses Secure Hash Algorithm (SHA)

  • The latest version, FIPS 186-3, also incorporates digital signature algorithms based on RSA and on elliptic curve cryptography

  • ONLY provides digital signature function: signature created for, private key

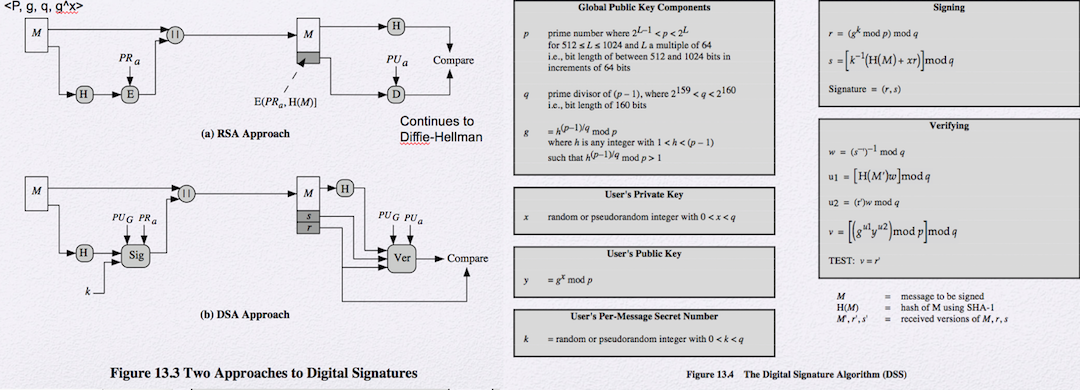The DSA approach also makes use of a hash function. The hash code is provided as input to a signature function along with a random number k generated for this particular signature. The signature function also depends on the sender’s private key (PRa ) and a set of parameters known to a group of communicating principals. We can consider this set to constitute a global public key (PUG ). The result is a signature consisting of two components, labeled s and r .

At the receiving end, the hash code of the incoming message is generated. This plus the signature is input to a verification function. The verification function also depends on the global public key as well as the sender’s public key (PUa ), which is paired with the sender’s private key. The output of the verification function is a value that is equal to the signature component r if the signature is valid. The signature function is such that only the sender, with knowledge of the private key, could have produced the valid signature.

The test at the end is on the value r , which does not depend on the message at all. Instead, r is a function of k and the three global public-key components. The multiplicative inverse of k (mod q ) is passed to a function that also has as inputs the message hash code and the user’s private key. The structure of this function is such that the receiver can recover r using the incoming message and signature, the public key of the user, and the global public key. It is certainly not obvious from Figure 13.4 or Figure 13.5 that such a scheme would work. A proof is provided in Appendix K.

Elliptic Curve Digital Signature Algorithm (ECDSA)

efficiency advantage of elliptic curve cryptography, which yields security comparable to that of other schemes with a smaller key bit length.

RSA Probabilistic Signature Scheme (RSA-PSS)

  • Included in the 2009 version of FIPS 186

  • Latest RSA scheme,reccomended by RSA Laboratories as the most secure

  • All schemes developed prior to PSS it hasn't been possible to develop a mathematical proof that the signature scheme is as secure as the underlying RSA encryption\/decryption primitive

  • First proposed by Bellare and Rogaway

  • This approach, unlike the other RSA-based schemes, introduces a randomization process that enables the security of the method to be shown to be closely related to the security of the RSA algorithm itself

  • Can be used for encryption\/key exchange

  • Because only the sender knows the private key, only the sender could have produced a valid signature

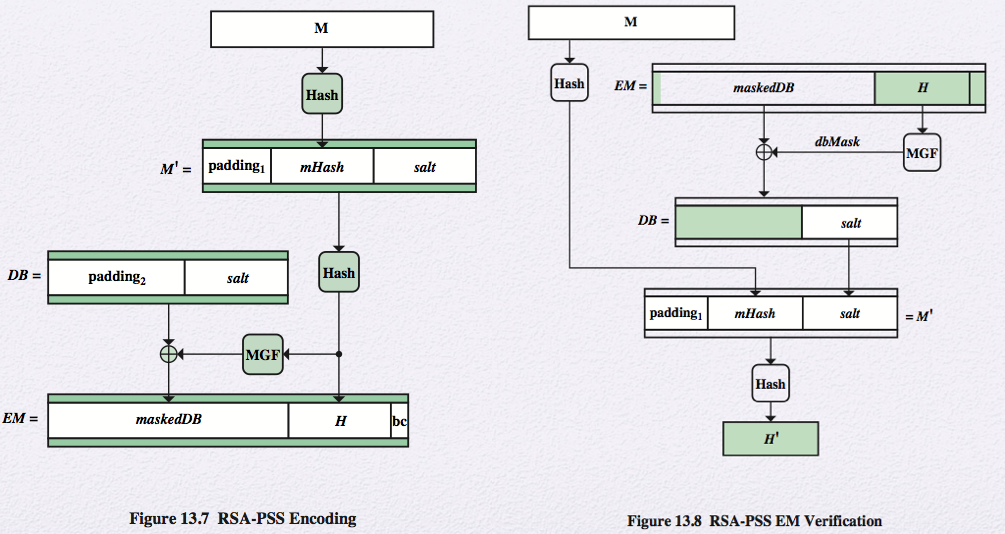
  • salt = pseudorandom number, changes with every use, signing the same message twice using the same private key to yield two different signatures (adds security)

  • M = message

  • EM = encoded message, fixed-length message digest

  • All of the RSA-based standardized digital signature schemes involve appending one or more constants (e.g., padding1 and padding2 ) in the process of forming the message digest. The objective is to make it more difficult for an adversary to find another message that maps to the same message digest as a given message or to find two messages that map to the same message digest

Mask Genreation Fucntion (MGF)

  • Typically based on a secure cryptographic hash function such as SHA-1

  • A cryptographically secure way of generating a message digest\/hash of variable length, based on an underlying cryptographic hash function(i.e. SHA-1) that produces a fixed-length output

  • MGF(X , maskLen ) is a pseudorandom function. X = bit string of any length, L = desired length in octets of the output.

results matching ""

    No results matching ""